Intergrowth Family AFX-LEV
Periodic Building Unit
| Periodic Building Unit (PerBU): | ABC-6 layer of hexagonally arranged (isolated) 6-rings | |||||
| Layer symmetry | P (6) m m | |||||
| 2D cell parameters | a = 13.05 Å | b = 13.05 Å | gamma = 120° | |||
| References |
|||
| Tsunoji, N., Gies, H., Funase, N., Kolb, U., Yokoi, T., Masahiro Sadakane, M. and Sano, T. | |||
| "Dual Templating for AFX/LEV Intergrowth Zeolite." | |||
| Chemistry Letters, 51, 121-123 (2022) | |||
Connectivity pattern
| Examples |
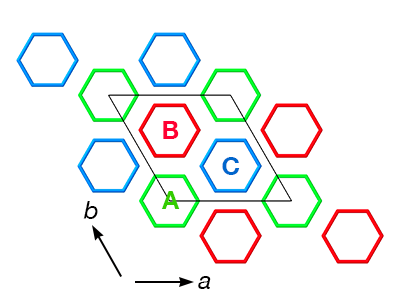 |
The layers are stacked along the [001] direction using the following connectivity patterns
| |||||||||||||||||||||
|
* relative to the first layer |
| Effect on channel system | |
| The disorder blocks the 8-ring channel of AFX along [001]. | |
Simplest ordered end members
The color of each layer reflects the translation used to generate it from the first layer (see table above).
-->
| Polymorph AFX | |||||
| Cell Parameters: | hexagonal | P 63/m m c: (# 194) | |||
| a = 13.6740 Å | b = 13.6740 Å | c = 19.6950 Å | |||
| α = 90.000° | β = 90.000° | γ = 120.000° | |||
| Volume = | 3189.2 Å3 | ||||
| Framework Density (FDSi): | 15.1 | ||||
| Ring sizes (# T-atoms): | 8 6 4 | ||
| Channel dimensionality: | Topological (pore opening > 6-ring): 3-dimensional | ||
| ABC-6 sequence: | AABBAACC sequence of ABC-6 layers | ||
| Maximum diameter of a sphere: | |||||||
| that can be included | 7.76 Å | ||||||
| that can diffuse along | a: 3.73 Å | b: 3.73 Å | c: 3.73 Å | ||||
| addional volume data | |||||||
| Composite Building Units: |
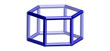 | 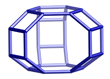 | 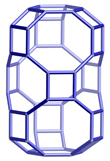 | ||||
d6r | gme | aft | ||||
| In this space group and setting, the PerBUs are stacked along [001] |
|||||
| Note: This polymorph corresponds to the ordered framework AFX | |
-->
| Polymorph LEV | |||||
| Cell Parameters: | trigonal | R -3 m:H (# 166) | |||
| a = 13.1680 Å | b = 13.1680 Å | c = 22.5780 Å | |||
| α = 90.000° | β = 90.000° | γ = 120.000° | |||
| Volume = | 3390.5 Å3 | ||||
| Framework Density (FDSi): | 15.9 | ||||
| Ring sizes (# T-atoms): | 8 6 4 | ||
| Channel dimensionality: | Topological (pore opening > 6-ring): 2-dimensional | ||
| ABC-6 sequence: | AABCCABBC sequence of ABC-6 layers | ||
| Maximum diameter of a sphere: | |||||||
| that can be included | 7.1 Å | ||||||
| that can diffuse along | a: 3.53 Å | b: 3.53 Å | c: 2.5 Å | ||||
| addional volume data | |||||||
| Composite Building Units: |
 | 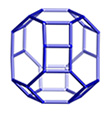 | |||
d6r | lev | |||
| In this space group and setting, the PerBUs are stacked along [001] |
|||||
| Note: This polymorph corresponds to the ordered framework LEV | |